General Prover / Verifier System

Purpose and Role

The General Prover / Verifier System is the cryptographic heart of LayerEdge’s verification architecture. It is responsible for recursively aggregating multiple normalized zk-proofs into a single succinct proof, dramatically reducing verification overhead.

By shifting computational effort to provers and compressing proof size, this system enables LayerEdge to provide a universal, scalable, and cost-effective zk-verification layer — verifiable natively on Bitcoin.

This module is essential to:

• Make zk-verification viable at scale
• Minimize on-chain costs and bandwidth
• Allow Bitcoin to act as the universal final settlement layer without needing to verify every individual proof directly

Core Components

1. Aggregation Circuits

Aggregation circuits are special zk-circuits that receive multiple zk-proofs as inputs and output a new, single zk-proof that asserts the correctness of all previous ones.

Each circuit is tailored to balance:

• Prover time
• Constraint efficiency
• Field compatibility
• Recursion depth

2. Recursive Composition Logic

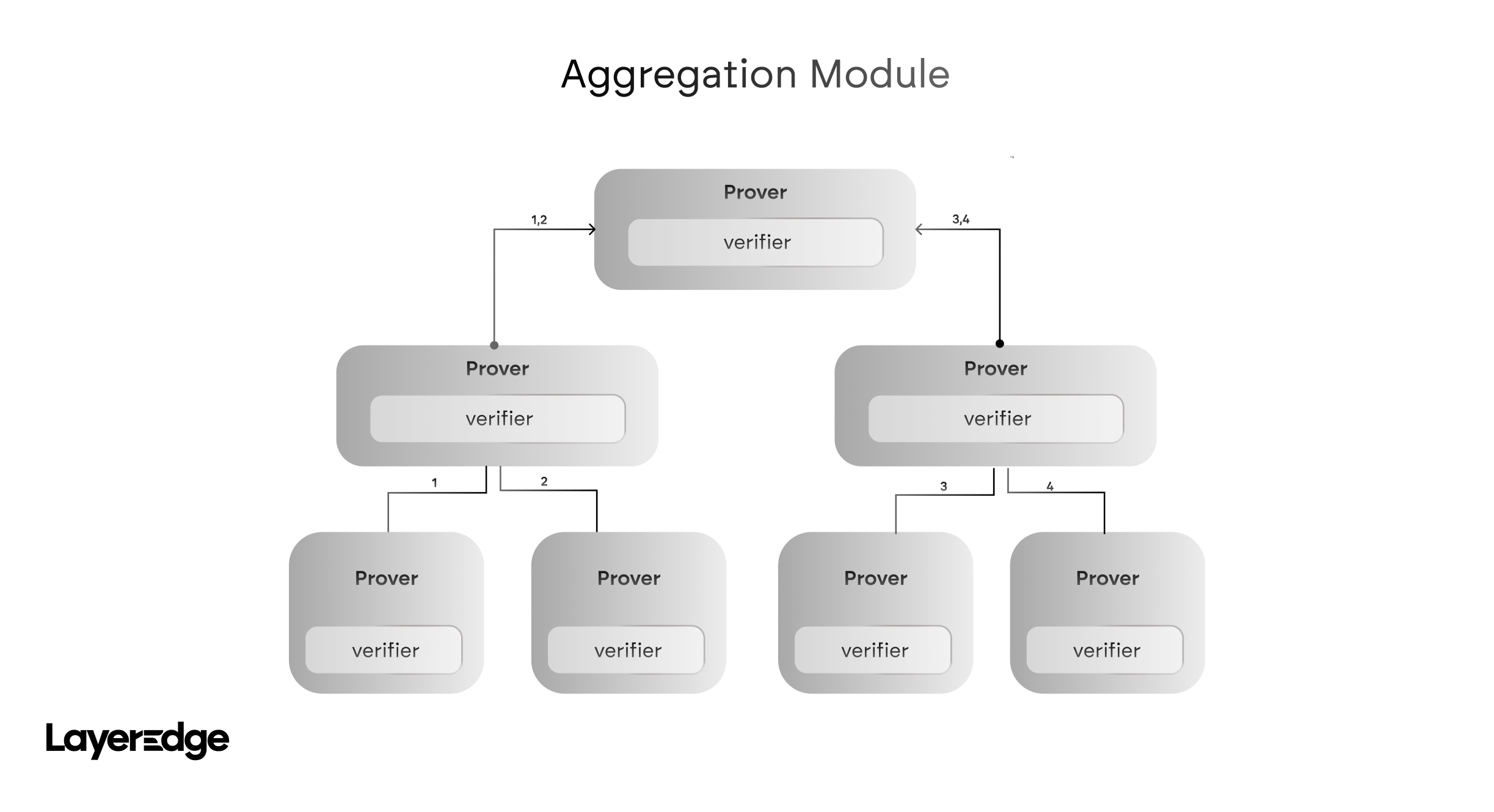
Recursive aggregation is built using binary or fan-in trees, where each level of the tree performs one round of proof aggregation.

• Leaf Verifications: Individual normalized zk-proofs
• Internal Verifications: Aggregation steps (pairwise or batched)
• Root Verification: Final output — a single zk-proof representing the validity of all the original inputs

This structure ensures:

• Logarithmic recursion depth
• High parallelism
• Efficient memory usage across large batches

---

Aggregation Mechanism

Pairwise Aggregation

Let:

• $\pi_A$ and $\pi_B$ be two zk-proofs

The aggregation circuit receives $(\pi_A, \pi_B)$ along with their public inputs and outputs a single proof $\pi_{AB}$. This proof internally verifies the validity of both $\pi_A$ and $\pi_B$, and encodes a combined validity statement.

This is repeated recursively until the full set is reduced to a single $\pi_{agg}$.

---

Multi-Proof Batching

Some implementations support batching multiple proofs at once (e.g., 8, 16, 32 proofs per round), reducing recursion depth further.

Advantages:

• Lower number of aggregation rounds
• Reduced memory overhead
• Fewer final circuit evaluations

Batching may require:

• Custom aggregation gates in the underlying circuit
• Polynomial commitment schemes like:
  • KZG (used in PLONK, for succinct SNARK aggregation)
  • FRI (used in STARKs, for scalable transparent batching)

---

Final Aggregated Proof

After log(n) steps, a single final proof is produced.

$$\pi_{agg} = \bigoplus(\pi_1, \pi_2, ..., \pi_n)V(\pi_{agg}) = \bigwedge_{i=1}^n V(\pi_i)$$

Where:

• $\bigoplus$ is the recursive aggregation function embedded in the circuit
• $V$ is the verification logic proving that each original zk-proof $\pi_i$ is valid

If $\pi_{agg}$ verifies correctly, then every $\pi_i$ has also been validated — with only a single proof and one verification call.

---

Performance Considerations

Constraint Optimization

Each aggregation circuit is optimized for low constraint count and fast recursive verification:

• R1CS minimization in Groth16 or Spartan-based circuits
• Custom gates for curve and hash operations (e.g., Poseidon, Rescue)
• No stdlib bloat — only essential constraints are compiled into each aggregation layer

This ensures:

• Provers can generate recursive proofs quickly
• Verifiers (especially on-chain or light clients) can validate with minimal cost

---

Prover vs Verifier Load

One of the core design principles of LayerEdge is to shift computational burden away from verifiers and toward provers.

• Provers handle recursive composition, curve arithmetic, hashing, and polynomial openings
• Verifiers simply check one small aggregated proof
• This trade-off makes the system scalable and friendly for low-resource verifiers (e.g., Light Nodes)

---

Parallel Aggregation Trees

LayerEdge’s recursive trees are designed for horizontal scaling:

• Subtrees can be aggregated in parallel across threads or machines
• Aggregator clients can split and merge branches independently
• Perfect for GPU, ASIC, or distributed proof-generation setups

This enables high-throughput batch verification — suitable for handling rollups, zk-oracles, and machine-learning ZK pipelines concurrently.

Key Benefits

Feature	Description
Recursive Aggregation	Scales to thousands of proofs with log(n) recursion steps
Minimal On-Chain Load	Only one final proof is submitted and verified
Parallelism	Subtrees can be built concurrently for high throughput
Efficient Circuit Design	Custom constraint logic for low prover/verifier cost
Strong Soundness Guarantees	Final $\pi_{agg}$ implies all input proofs are valid

Summary

The General Prover / Verifier System turns LayerEdge into a scalable zk-verification fabric, where:

• zk-proofs from any protocol are ingested
• Recursively aggregated into a single succinct proof
• Efficiently verified by Bitcoin or LayerEdge Light Nodes

This system is what makes the vision of trustless, cost-efficient, Bitcoin-secured computation at scale possible.